750. Home
by trains
One of the teams
participating in the Olympic Games has decided to return home by trains. The
guys wanted to get home as soon as possible. Unfortunately, not all the trains
come from the Olympic city to the
station, where the boys live. And what's even more insulting, not all the
trains passing through the stations, stop at them (in general, the train does
not stop at all the stations which passes).
The stations in a line are
numbered with integers from 1 to n.
The station number 1 is located in the city, home of the Olympics, and at time
0, guys come to the station. The station where the guys want to get has the
number e.
Write a program that by
the schedule of the trains calculates the minimum time the guys can get home.
Input. Initially the numbers n (2 ≤ n ≤
100) and e (2 ≤ e ≤ n) are given. Next number m
(0 ≤ m ≤ 100) denotes the number of train routes. Then the
description of m routes is given. The
description of each route starts with
the number ki (2 ≤ ki ≤ n)
– the number of stations where it stops, and then ki pairs of
numbers, the first one gives the station number, and the second one gives the
time when the train stops here (the time is an integer from the interval from 0 to 109). The stations of
one route are sorted in ascending order of time. In one route the train always
moves in one direction – either from the Olympic city or to the Olympic city.
Output. Print one number – the
minimum time in which the children can achieve their station. If its impossible
to go home using the existed number of routes, print -1.
|
Sample
input |
Sample
output |
|
5 3 4 2 1 5 2 10 2 2 10 4 15 4 5 0 4 17 3
20 2 35 3 1 2 3 40 4 45 |
20 |
SOLUTION
graphs – Dijkstra algorithm
Анализ алгоритма
Построим граф, количество вершин которого равно числу
станций. Каждое ребро графа соответствует перемещению одной электрички между
соседними станциями, на которых она останавливается. Если стартовав со станции i
в момент времени From, электричка приезжает на соседнюю станцию j
в момент времени To, то проведем от i до j ориентированное
ребро, записав на нем пару чисел (From, To). Граф будем задавать
списком смежности, поэтому каждому ребру следует еще приписать номер вершины,
куда оно направлено.
Запускаем алгоритм Дейкстры на построенном ориентированном
графе. Ищем кратчайший путь от вершины 1 до
вершины e.
Пример
Имеется пять станций и расписание движения четырех
электричек.
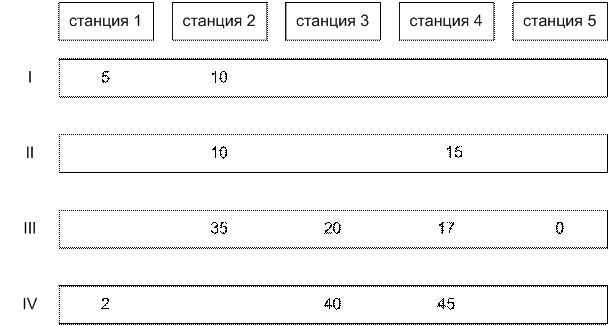
Соответствующий
граф имеет вид:

Реализация алгоритма
Алгоритм
Дейкстры реализуем при помощи очереди с приоритетами. Элементами очереди будут
пары (время за которое можно добраться от истока, номер вершины).
Таким образом, первой в очереди всегда будет вершина, в которую мы раньше всего
доберемся от истока (стартовая вершина, из которой запускается алгоритм
Дейкстры). Объявим класс Prior, содержащий эту пару (Time, Vertex).
Переопределим операторы сравнения меньше и больше: та пара считается меньшей, у
которой расстояние до истока Dist меньше.
class Prior
{
public:
int Time,
Vertex;
Prior(int
Time, int Vertex) : Time(Time), Vertex(Vertex)
{}
int operator< (const
Prior &a) const
{
return Time
< a.Time;
}
int operator> (const
Prior &a) const
{
return Time
> a.Time;
}
};
Объявим класс
ребро, соединяющие две соседние станции. Оно содержит следующие атрибуты:
·
vTo – номер станции, куда едет электричка;
·
timeFrom – время отправления электрички из текущей станции;
·
timeTo – время прибытия электрички на станцию vTo;
class Edge
{
public:
int vTo,
timeFrom, timeTo;
Edge(int vTo,
int timeFrom, int
timeTo)
: vTo(vTo), timeFrom(timeFrom),
timeTo(timeTo) {}
};
Объявим класс
граф. Он содержит количество вершин n и задается списком смежности g.
class Graph
{
public:
int n;
vector<vector<Edge> > g;
Graph(int n =
1) : n(n)
{
g = vector<vector<Edge> >(n);
}
Функция добавления ориентированного
ребра (From, To). Электричка выезжает со станции From в
момент времени timeFrom и
прибывает на станцию To в момент времени timeTo.
void AddEdge(int From, int To, int timeFrom, int
timeTo)
{
g[From].push_back(Edge(To,timeFrom,timeTo));
}
Алгоритм Дейкстры запускается из
вершины Source. Вторым аргументом передается массив time: time[i]
содержит наименьшее время, за которое можно добраться на электричках из вершины
Source в i.
void
Dijkstra(int Source, vector<int> &time)
{
priority_queue<Prior,
vector<Prior>, greater<Prior> > pq;
Кладем в очередь
пару (0, Source), полагаем время time[Source] равным 0 (добраться
от вершины Source до ее же самой можно за нулевое время).
pq.push(Prior(0,Source)); time[Source] = 0;
while(!pq.empty())
{
int v =
pq.top().Vertex;
int d =
pq.top().Time; pq.pop();
Проверяем, не является ли извлеченная
из головы очереди пара (v, d) фиктивной.
if (d >
time[v]) continue;
Просматриваем вершины to,
смежные с v. Пробуем провести релаксацию ребра (v, to).
for(int i = 0; i < g[v].size(); i++)
{
time[v] содержит наименьшее
время, за которое можно доехать до станции v. Если ребро (v, to)
содержит информацию, что электричка выезжает из v в to раньше,
чем time[v], то мы на эту электричку не успеваем.
if
(g[v][i].timeFrom < time[v]) continue;
Вычисляем станцию to, в
которое ведет ребро.
int to
= g[v][i].vTo ;
Если до станции to по ребру (v,
to) можно добраться за меньшее время, нежели уже имеется в time[to],
то проводим релаксацию и заносим пару (time[to], to) в очередь.
if
(time[to] > g[v][i].timeTo)
{
time[to] = g[v][i].timeTo;
pq.push(Prior(time[to],to));
}
}
}
}
};
Объявим
указатель на граф.
Graph *g;
Основная часть
программы. Инициализируем массив time, содержащий кратчайшее время, за которое
можно добраться до всех станций из начальной.
scanf("%d %d %d",&n,&e,&m);
g = new Graph(n+1);
time =
vector<int>(n+1,INF);
Читаем входные данные. Строим граф g.
for(i = 0; i < m; i++)
{
scanf("%d",&stations);
PrevStation = -1;
for(j = 0; j
< stations; j++)
{
scanf("%d
%d",&CurStation,&CurTime);
Электричка выезжает со станции PrevStation
в момент времени PrevTime и движется на следующую станцию CurStation,
на которую прибывает в момент времени CurTime.
if
(PrevStation != -1) g->AddEdge(PrevStation,CurStation,
PrevTime,CurTime);
PrevStation = CurStation; PrevTime =
CurTime;
}
}
Запускаем алгоритм Дейкстры из
вершины 1.
g->Dijkstra(1,time);
Выводим ответ.
if (time[e] == INF) printf("-1\n");
else printf("%d\n",time[e]);